Most CNN architectures have been developed to attain the best accuracy on ImageNet. Computing power is not limited for this competition, why bother?

However you may want to run your model on an old laptop, maybe without GPU, or even on your mobile phone. Let’s see three CNN architectures that are efficient while sacrificing little accuracy performance.

1. MobileNet

Arxiv link: (Howard et al, 2017)

MobileNet uses depthwise separable convolutions. This convolution block was at first introduced by Xception (Chollet, 2016). A depthwise separable convolution is made of two operations: a depthwise convolution and a pointwise convolution.

A standard convolution works on the spatial dimension of the feature maps and on the input and output channels. It has a computational cost of $D_f^2 * M * N * D_k^2$; with $D_f$ the dimension of the input feature maps, $M$ and $N$ the number of input and output channels, and $D_k$ the kernel size.

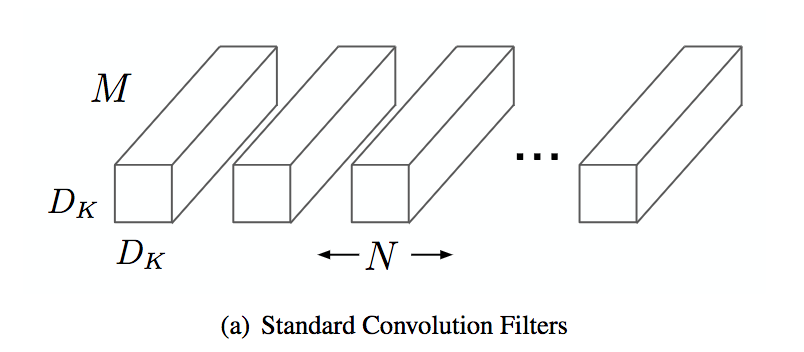
A depthwise convolution maps a single convolution on each input channel separately. Therefore its number of output channels is the same of the number of input channels. Its computational cost is $D_f^2 * M * D_k^2$.

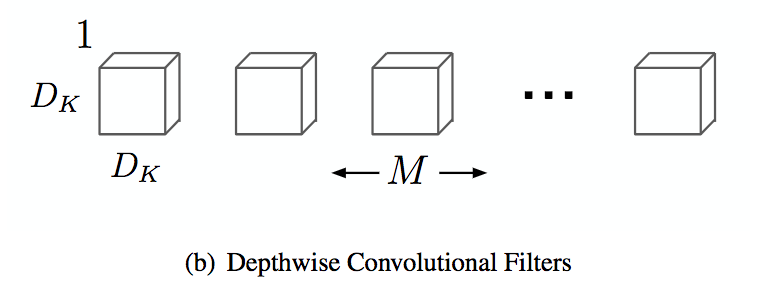
The last operation is a pointwise convolution. It is a convolution with a kernel size of 1x1 that simply combines the features created by the depthwise convolution. Its computational cost is $M * N * D_f^2$.

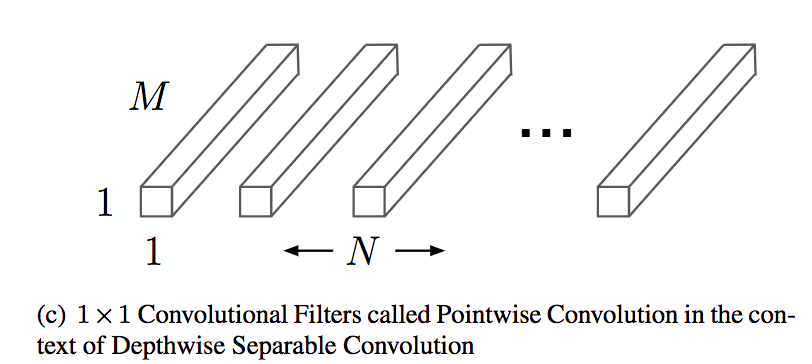
The computational cost of the depthwise separable convolution is the sum of the costs of the depthwise and pointwise operations. Compared to a standard convolution it offers a computation reduction of $\frac{1}{N} + \frac{1}{D_k^2}$. With a kernel size of 3x3, it results in 8 times less operations!

MobileNet also provides two parameters allowing to reduce further more its number of operations:

The width multiplier (between 0 and 1) thins the number of channels. At each layer instead of producing $N$ channels, it will produce $\alpha * N$. This multiplier can be used to handle a trade-off between the desired latency and the performance.

Another multiplier exists: the resolution multiplier. It scales the input size of the image, between 224 to 128. Because the MobileNet uses a global average pooling instead of a flatten, you can train your MobileNet on 224x224 images, then use it on 128x128 images! Indeed with a global pooling, the fully connected classifier at the end of the network depends only the number of channels not the feature maps spatial dimension.

2. ShuffleNet

Arxiv link: (Zhang et al, 2017)

ShuffleNet introduces the three variants of the Shuffle unit. It is composed of group convolutions and channel shuffles.

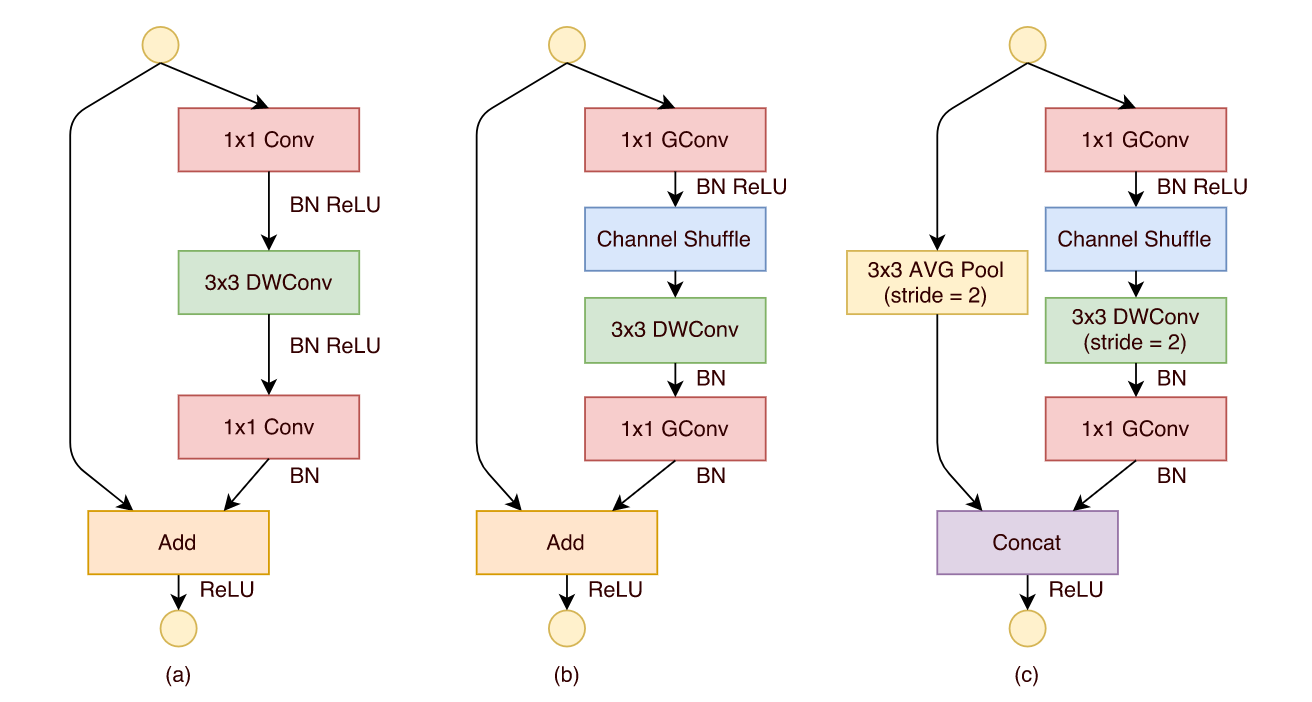
A group convolution is simply several convolutions, each taking a portion of the input channels. In the following image you can see a group convolution, with 3 groups, each taking one of the 3 input channels.

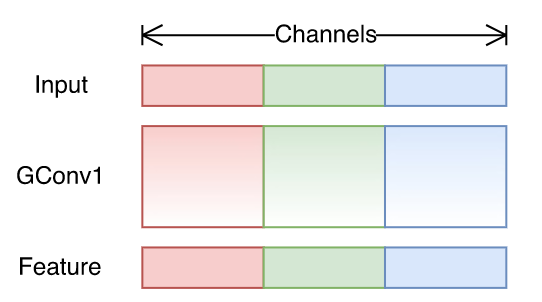
It was at first introduced by AlexNet (Krizhevsky et al, 2012) to split a network into two GPUs.

It greatly diminishes the computational cost. Let us take a practicable example: If there are 4 input channels, and 8 output channels and we choose to have two groups, each taking 2 input channels and 4 output channels.

With one group the computational cost would be $D_f^2 * D_k^2 * 4 * 8$, while with two groups the cost is $(D_f^2 * D_k^2 * 2 * 4) * 2$ or $D_f^2 * D_k^2 * 4 * 4$. Half as many operations! The authors reached best results with 8 groups, thus the reduction is even more important.

Finally the authors add a channel shuffle that randomly mix the output channels of the group convolution. The trick to produce this randomness can be seen here.

3. EffNet

Arxiv link: (Freeman et al, 2018)

EffNet uses spatial separable convolutions. It is similar to MobileNet’s depthwise separable convolutions.

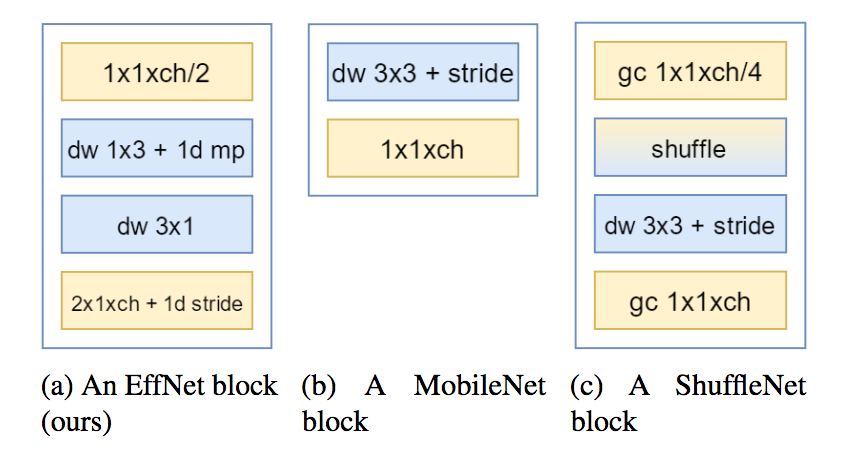
The separable depthwise convolution is the rectangle colored in blue for EffNet block. It is made of depthwise convolution with a line kernel (1x3), followed by a separable pooling, and finished by a depthwise convolution with a column kernel (3x1)

Let’s see the computational gain. A normal depthwise with a 3x3 kernel would have a cost of $3^2 * D_f^2 * M$. The first depthwise with a 1x3 kernel has a computational cost of $3 * D_f^2 * M$. The separable pooling halves the feature maps height and has a marginal cost. The second depthwise, with a 3x1 kernel, has then a cost of $3 * \frac{D_f^2}{2} * M$. Thus the whole cost is $1.5 * (3 * D_f^2 * M)$. Half less than the normal depthwise!

Another optimization done by EffNet over MobileNet and ShuffleNet, is the absence of “normal convolution” at the beginning:

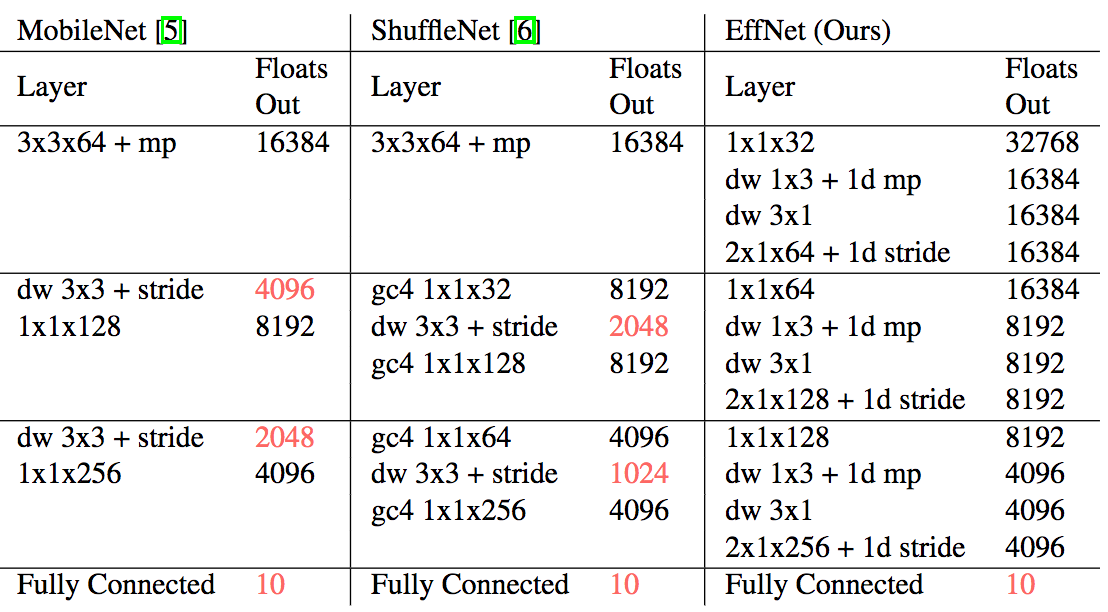
To quote the authors (emphasis mine):

Both MobileNet and ShuffleNet avoided replacing the first layer with the claim that this layer is already rather cheap to begin with. We respectfully disagree with this claim and believe that every optimisation counts. After having optimised the rest of the layers in the network, the first layer becomes proportionally larger. In our experiments, replacing the first layer with our EffNet block saves ∼ 30% of the computations for the respective layer.

4. Conclusion

MobileNet, ShuffleNet, and EffNet are CNN architectures conceived to optimize the number of operations. Each replaced the standard convolution with their own version.

MobileNet (github) depthwise separable convolution uses a depthwise convolution followed by a pointwise convolution. In a addition it introduces two hyperparameters: the width multiplier that thins the number of channels, and the resolution multiplier that reduces the feature maps spatial dimensions.

ShuffleNet (github) uses pointwise convolution in groups. In order to combine the features produced by each group, a shuffle layer is also introduced.

Finally EffNet (github) uses spatial separable convolution, which is simply a depthwise convolution splitted along spatial axis with a separable pooling between them.

This article was at first published in Towards Data Science and has also been translated in Chinese!