This post contains the notes taken from the following paper:
- Deep Learning Scaling Is Predictable, Empirically by Baidu Research.
The last years in Deep Learning have seen a rush to gigantism:
- Models are becoming deeper and deeper from the 8 layers of AlexNet to the 1001-layer ResNet.
- Training on large dataset is way quicker, ImageNet can now (with enough computing power) been trained in less than 20 minutes.
- Dataset size are increasing each year.
As this paper rightly declare in its introduction:
The Deep Learning (DL) community has created impactful advances across diverse application domains by following a straightforward recipe: search for improved model architectures, create large training data sets, and scale computation.
However it also notes that new models and hyperparameters configuration are often depend on epiphany and serendipity.
In order to harness the power of big data (more data, more computation power, etc.) models should not be designed to reduce error rate of an epsilon on Imagenet but be designed to be better with more data.
Baidu Research introduce a power-law expononent, that measure the steepness of the learning curve:
$$\epsilon(m) \propto \alpha m^{\beta_g}$$
Where $\epsilon(m)$ is the generalization error on the number of train samples $m$; $\alpha$ a constant related to the problem; and $\beta_g$ the steepness of the learning curve.
$\beta_g$ is said to settle between -0.07 and -0.35.
The Methodology
Baidu tested four domains: machine translation, language modeling, image classification, and speech recognition.
For each domain, a variety of architectures, optimizers, and hyperparameters is tested. To see how models scale with dataset size, Baidu trained models on samples ranging from 0.1% of the original data to the whole data (minus the validation set).
The paper’s authors try to find the smallest model that is able to overfit each sample.
Baidu also removed any regularizations, like weight decay, that might reduce the model’s effective capacity.
Results
In all domain, they found that the model size growth with dataset size sublinearly.
| Domain | Learning Curve Steepness $\beta_g$ |
|---|---|
| Machine Translation | -0.128 |
| Language Modeling | [-0.09, -0.06] |
| Image (top-1) | -0.309 |
| Image (top-5) | -0.488 |
| Speech | -0.299 |
The first thing that we can conclude from these numbers is that text based problems (translation and language modeling) scale badly faced to image problems.
It is worth noting that (current) models seem to scale better depending on the data dimension: Image and speech are of a higher dimensionality than text.
You may also wonder why image has two entries in the table. One for top-1 generalization error, and one for top-5. This is one of the most interesting finding of this paper. Current models of image classification improve their top-5 faster than top-1 as data size increases! I wonder the reason why.
Implications
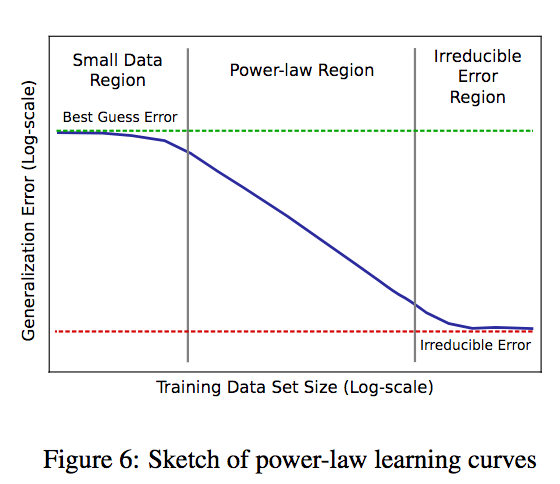
The authors separate the generalization error per data size in three areas:
- The small data region, where models given so few data can only make random guessing.
- The power law region, where models follow the power law. However the learning curve steepness may be improved.
- The irreductible error, a combination of the Bayes error (on which the model cannot be improved) and the dataset defects that may impair generalization.
The authors also underline major implications of the power law:
Given the power law, researchers can train their new architecture on a small dataset, and have a good estimation of how it would scale on a bigger dataset. It may also give a reasonable estimation of the hardware and time requirements to reach a chosen generalization error.
Instead of simply trying to improve a model’s accuracy, the authors suggest that beating the power law should be the end goal. Dataset size is going to grow each year, a scalable model would thrive in this situation. The authors advise methods that may help to extract more info on less data:
We suggest that future work more deeply analyze learning curves when using data handling techniques, such as data filtering/augmentation, few-shot learning, experience replay, and generative adversarial networks.
Baidu also recommends to search how to push the boundaries of the irreductible error. To do that we should be able to distinguish between what contributes to the bayes error, and what’s not.
Summary
Baidu Research showed that models follow a power law curve. They empirically determined the power law exponent, or steepness of the learning curve, for machine translation, language modeling, image classification, and speech recognition.
This power law express how much a model can improve given more data. Models for text problems are currently the less scalable.